MinDriver steps#

In this tutorial, we show how we can save individual steps during minimisation as well as how we can analyse them. We are going to minimise a simple system object. For details on how to define a system object, please have a look at other tutorials.

[1]:

import discretisedfield as df
import micromagneticmodel as mm

import oommfc as mc

region = df.Region(p1=(-50e-9, -50e-9, 0), p2=(50e-9, 50e-9, 10e-9))
mesh = df.Mesh(region=region, cell=(5e-9, 5e-9, 5e-9))

system = mm.System(name="mindriver_steps")

system.energy = mm.Zeeman(H=(0, 0, 1e5))
system.m = df.Field(mesh, nvdim=3, value=(1, 0, 0), norm=1.1e6)

We now have a system object and we can minimise it using MinDriver. By default, MinDriver saves only the data of the last step in the relexation. However, if we want to save all individual steps in between, we have to pass output_step=True to the drive method.

[2]:

md = mc.MinDriver()
md.drive(system, output_step=True)

Running OOMMF (ExeOOMMFRunner)[2025-02-02T14:32:11]... (0.5 s)

If we have a look at the table, we can see that multiple steps are saved:

[3]:

system.table.data

[3]:
max_mxHxm E delta_E bracket_count line_min_count conjugate_cycle_count cycle_count cycle_sub_count energy_calc_count E_zeeman iteration stage_iteration stage mx my mz
0 1.000000e+05 0.000000e+00 0.000000e+00 0.0 0.0 1.0 1.0 0.0 1.0 0.000000e+00 0.0 0.0 0.0 1.000000e+00 0.0 0.000000
1 9.999996e+04 -1.206285e-20 -1.206285e-20 1.0 0.0 1.0 1.0 0.0 2.0 -1.206285e-20 1.0 1.0 0.0 9.999996e-01 0.0 0.000873
2 9.848078e+04 -2.400340e-18 -2.388277e-18 2.0 0.0 1.0 1.0 0.0 3.0 -2.400340e-18 2.0 2.0 0.0 9.848078e-01 0.0 0.173648
3 9.396926e+04 -4.727747e-18 -2.327407e-18 3.0 0.0 2.0 2.0 0.0 4.0 -4.727747e-18 3.0 3.0 0.0 9.396926e-01 0.0 0.342020
4 8.660254e+04 -6.911504e-18 -2.183757e-18 4.0 0.0 3.0 3.0 0.0 5.0 -6.911504e-18 4.0 4.0 0.0 8.660254e-01 0.0 0.500000
5 7.660444e+04 -8.885258e-18 -1.973754e-18 5.0 0.0 4.0 4.0 0.0 6.0 -8.885258e-18 5.0 5.0 0.0 7.660444e-01 0.0 0.642788
6 6.427876e+04 -1.058904e-17 -1.703780e-18 6.0 0.0 5.0 5.0 0.0 7.0 -1.058904e-17 6.0 6.0 0.0 6.427876e-01 0.0 0.766044
7 5.000000e+04 -1.197108e-17 -1.382038e-18 7.0 0.0 6.0 6.0 0.0 8.0 -1.197108e-17 7.0 7.0 0.0 5.000000e-01 0.0 0.866025
8 3.464669e+04 -1.296684e-17 -9.957653e-19 8.0 0.0 7.0 7.0 0.0 9.0 -1.296684e-17 8.0 8.0 0.0 3.464669e-01 0.0 0.938062
9 3.420201e+04 -1.298938e-17 -2.253721e-20 9.0 0.0 7.0 7.0 0.0 10.0 -1.298938e-17 9.0 9.0 0.0 3.420201e-01 0.0 0.939693
10 1.981052e+04 -1.354905e-17 -5.596679e-19 10.0 0.0 8.0 8.0 0.0 11.0 -1.354905e-17 10.0 10.0 0.0 1.981052e-01 0.0 0.980181
11 1.736482e+04 -1.361301e-17 -6.395896e-20 11.0 0.0 8.0 8.0 0.0 12.0 -1.361301e-17 11.0 11.0 0.0 1.736482e-01 0.0 0.984808
12 6.305027e+03 -1.379550e-17 -1.824996e-19 12.0 0.0 9.0 9.0 0.0 13.0 -1.379550e-17 12.0 12.0 0.0 6.305027e-02 0.0 0.998010
13 3.143399e-11 -1.382301e-17 -2.750291e-20 13.0 0.0 9.0 9.0 0.0 14.0 -1.382301e-17 13.0 13.0 0.0 3.143399e-16 0.0 1.000000

Using all the utility of the Table object, we can analyse the data. For instance, we can plot the energy.

[4]:

system.table.mpl(y=["E"])
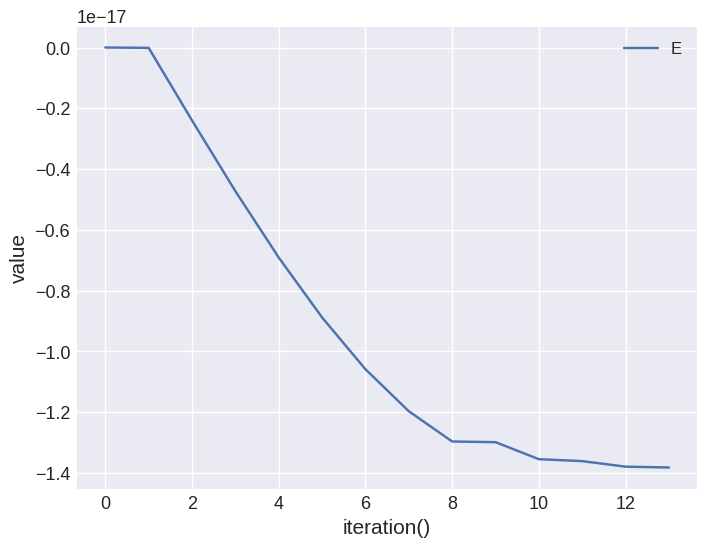
../../../_images/documentation_notebooks_oommfc_mindriver-steps_7_0.png

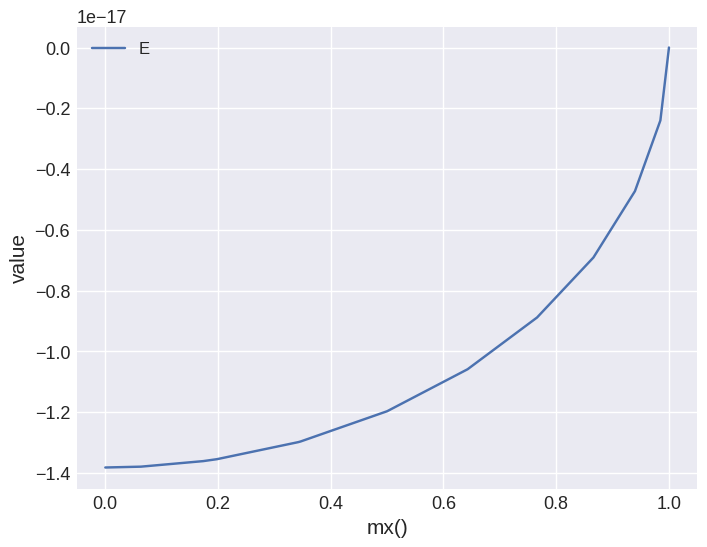
By fecault, iteration is showed on the \(x\)-axis. We can change that by passing x variable. For example:

[5]:

system.table.mpl(x="mx", y=["E"])
../../../_images/documentation_notebooks_oommfc_mindriver-steps_9_0.png

micromagneticdata analysis#

Similar to all other drivers, we can use micromagneticdata package to analyse the data. We start by creationg the data object:

[6]:

import micromagneticdata as md

data = md.Data(name=system.name)

We can have a look at all drives we did so far:

[7]:

data.info

[7]:
drive_number date time driver t n n_threads adapter start_time adapter_version output_step end_time elapsed_time success
0 0 2023-01-16 17:35:54 MinDriver NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
1 1 2023-01-16 17:35:58 TimeDriver 2.000000e-09 200.0 4.0 NaN NaN NaN NaN NaN NaN NaN
2 2 2023-01-16 17:37:00 MinDriver NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
3 3 2023-01-16 17:37:04 TimeDriver 2.000000e-09 200.0 4.0 NaN NaN NaN NaN NaN NaN NaN
4 4 2023-01-16 17:37:28 MinDriver NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
5 5 2023-01-16 17:38:02 MinDriver NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
6 6 2023-01-16 17:38:06 TimeDriver 2.000000e-09 200.0 4.0 NaN NaN NaN NaN NaN NaN NaN
7 7 2023-10-10 16:55:09 MinDriver NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
8 8 2023-10-10 16:55:13 TimeDriver 2.000000e-09 200.0 4.0 NaN NaN NaN NaN NaN NaN NaN
9 9 2023-10-18 12:37:23 MinDriver NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
10 10 2023-10-18 12:39:38 MinDriver NaN NaN NaN NaN NaN NaN NaN NaN NaN NaN
11 11 2023-10-18 12:39:56 TimeDriver 2.000000e-09 200.0 4.0 NaN NaN NaN NaN NaN NaN NaN
12 12 2024-07-14 16:10:32 MinDriver NaN NaN NaN oommfc NaN NaN NaN NaN NaN NaN
13 13 2024-07-14 16:10:37 TimeDriver 2.000000e-09 200.0 4.0 oommfc NaN NaN NaN NaN NaN NaN
14 14 2025-02-02 14:11:40 MinDriver NaN NaN NaN oommfc 2025-02-02T14:11:40 0.64.1 True 2025-02-02T14:11:41 00:00:01 True
15 15 2025-02-02 14:11:46 TimeDriver 2.000000e-09 200.0 4.0 oommfc 2025-02-02T14:11:46 0.64.1 NaN NaN NaN NaN
16 16 2025-02-02 14:14:09 MinDriver NaN NaN NaN oommfc 2025-02-02T14:14:09 0.64.1 True 2025-02-02T14:14:10 00:00:01 True
17 17 2025-02-02 14:14:14 TimeDriver 2.000000e-09 200.0 4.0 oommfc 2025-02-02T14:14:14 0.64.1 NaN 2025-02-02T14:14:15 00:00:02 True
18 18 2025-02-02 14:32:10 MinDriver NaN NaN NaN oommfc 2025-02-02T14:32:10 0.65.0 True 2025-02-02T14:32:11 00:00:01 True

There is only one drive and we can get it by passing 0 (ot -1) as an index:

[8]:

drive = data[0]

We can now plot the magnetisation at individual iterations, by indexing it again with the step number and do all usual operations allowed by discretisedfield.Field object.

[9]:

drive[0]

[9]:
Field
  • Mesh
    • Region
      • pmin = [-5e-08, -5e-08, 0.0]
      • pmax = [5e-08, 5e-08, 1e-08]
      • dims = ['x', 'y', 'z']
      • units = ['m', 'm', 'm']
    • n = [20, 20, 2]
  • nvdim = 3
  • vdims:
    • x
    • y
    • z
  • unit = A/m

The number of steps in the drive is:

[10]:

drive.n

[10]:

14

Let us now create an interactive plot. For details on how to create custom interactive plots, please have a look at other tutorials.

[11]:

drive.register_callback(lambda f: f.sel("y")).hv(kdims=["x", "z"]).opts(frame_width=800)

[11]:
On this page
Try online:
Try locally:

This Page