Field operations 2#

In this notebook, we show (and compare) computing individual energy terms:

[1]:

import discretisedfield as df
import micromagneticmodel as mm
import oommfc as mc

As an example, we use skyrmion magnetisation field.

[2]:

# Geometry
L = 100e-9
thickness = 5e-9
cell = (5e-9, 5e-9, 5e-9)
p1 = (-L/2, -L/2, 0)
p2 = (L/2, L/2, thickness)
region = df.Region(p1=p1, p2=p2)
mesh = df.Mesh(region=region, cell=cell, bc="xy")

# Parameters
Ms = 3.84e5
A = 8.78e-12
D = 1.58e-3
K = 1e4
u = (0, 0, 1)
H = (0, 0, 1e5)
system = mm.System(name='skyrmion')
system.energy = mm.Exchange(A=A) + mm.DMI(D=D, crystalclass='T') + mm.Zeeman(H=H) + mm.UniaxialAnisotropy(K=K, u=u)

def m_initial(point):
    x, y, z = point
    if x**2 + y**2 < (L/4)**2:
        return (0, 0, -1)
    else:
        return (0, 0, 1)

system.m = df.Field(mesh, nvdim=3, value=m_initial, norm=Ms)

md = mc.MinDriver()
md.drive(system)

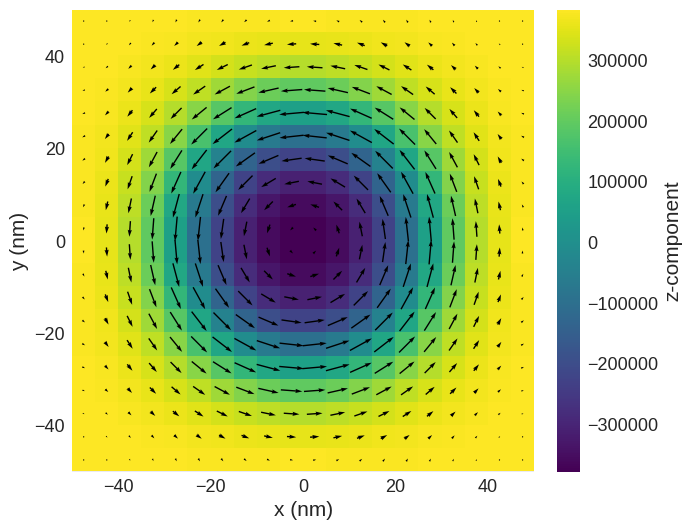
system.m.sel('z').mpl(figsize=(9, 7))

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.4 s)
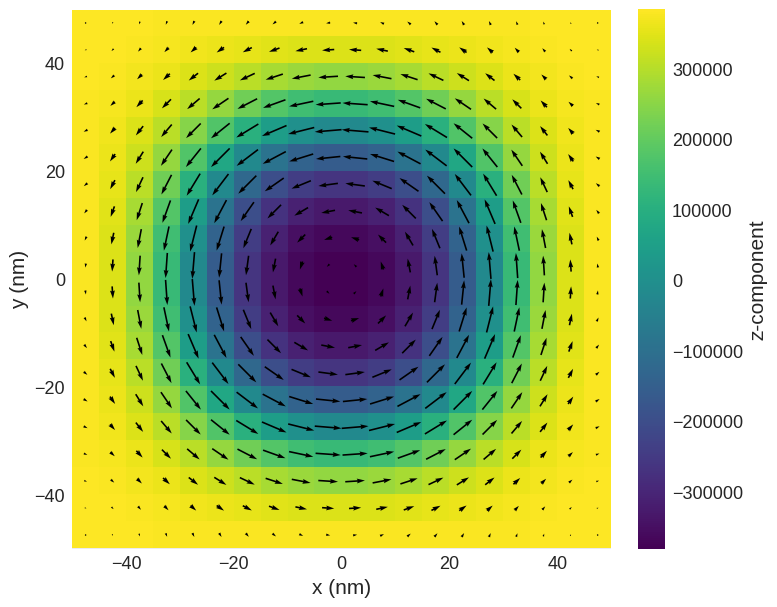
../../_images/examples_notebooks_field-operations2_3_1.png

Magnetisation#

\[\mathbf{m} = \frac{\mathbf{M}}{M_\text{s}}\]
[3]:

m = system.m.orientation

m.sel('z').mpl(scalar_kw={'clim': (-1, 1)})
../../_images/examples_notebooks_field-operations2_5_0.png

Zeeman#

property

equation in continuous form

discretisedfield form

Energy density

\(w = -\mu_{0}M_\text{s}\mathbf{m}\cdot\mathbf{H}\)

- mu0 * Ms * m.dot(H)

Energy

\(E = -\int_{V}\mu_{0}M_\text{s}\mathbf{m}\cdot\mathbf{H} dV\)

(- mu0 * Ms * m.dot(H)).integrate()

Effective field

\(\mathbf{H}_\text{eff} = \mathbf{H}\)

H

Energy density#

[4]:

wdf = - mm.consts.mu0 * Ms * m.dot(H)
wmc = mc.compute(system.energy.zeeman.density, system)
wdf.allclose(wmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.3 s)

[4]:

True

Energy#

[5]:

Edf = (- mm.consts.mu0 * Ms * m.dot(H)).integrate()
Emc = mc.compute(system.energy.zeeman.energy, system)
print(f'df: {Edf}')
print(f'mc: {Emc}')
print(f'rerr: {abs(Edf-Emc)/Edf * 100} %')

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.2 s)
df: [-1.03472186e-18]
mc: -1.03472185984e-18
rerr: [-1.62901158e-10] %

Effective field#

[6]:

Hdf = df.Field(mesh, nvdim=3, value=H)
Hmc = mc.compute(system.energy.zeeman.effective_field, system)
Hdf.allclose(Hmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.2 s)

[6]:

True

Uniaxial anisotropy#

property

equation in continuous form

discretisedfield form

Energy density

\(w = K |\mathbf{m} \times \mathbf{u}|^{2}\)

K * abs(m.cross(u)).dot(abs(m.cross(u)))

Energy

\(E = \int_{V}K |\mathbf{m} \times \mathbf{u}|^{2} dV\)

(K * abs(m.cross(u)).dot(abs(m.cross(u)))).integrate()

Effective field

\(\mathbf{H}_\text{eff} = \frac{2K}{\mu_{0}M_\text{s}} (\mathbf{m} \cdot \mathbf{u})\mathbf{u}\)

2 * K / (mm.consts.mu0 * Ms) * (m.dot(u)) * u

Energy density#

[7]:

wdf = K * abs(m.cross(u)).dot(abs(m.cross(u)))
wmc = mc.compute(system.energy.uniaxialanisotropy.density, system)
wdf.allclose(wmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.3 s)

[7]:

True

Energy#

[8]:

Edf = (K * abs(m.cross(u)).dot(abs(m.cross(u)))).integrate()
Emc = mc.compute(system.energy.uniaxialanisotropy.energy, system)
print(f'df: {Edf}')
print(f'mc: {Emc}')
print(f'rerr: {abs(Edf-Emc)/Edf * 100} %')

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.3 s)
df: [2.0433559e-19]
mc: 2.04335590117e-19
rerr: [7.9679366e-11] %

Effective field#

[9]:

Hdf = 2 * K / (mm.consts.mu0 * Ms) * (m.dot(u)) * u
Hmc = mc.compute(system.energy.uniaxialanisotropy.effective_field, system)
Hdf.allclose(Hmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.2 s)

[9]:

True

Exchange#

property

equation in continuous form

discretisedfield form

Energy density

\(w = - A \mathbf{m} \cdot \nabla^{2} \mathbf{m}\)

- A * m.dot(m.laplace)

Energy

\(E = -\int_{V} A \mathbf{m} \cdot \nabla^{2} \mathbf{m} dV\)

(- A * m.dot(m.laplace)).integrate()

Effective field

\(\mathbf{H}_\text{eff} = \frac{2A}{\mu_{0}M_\text{s}} \nabla^{2} \mathbf{m}\)

2 * A / (mu0 * Ms) * m.laplace

Energy density#

[10]:

wdf = - A * m.dot(m.laplace)
wmc = mc.compute(system.energy.exchange.density, system)
wdf.allclose(wmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.3 s)

[10]:

True

Energy#

[11]:

Edf = (- A * m.dot(m.laplace)).integrate()
Emc = mc.compute(system.energy.exchange.energy, system)
print(f'df: {Edf}')
print(f'mc: {Emc}')
print(f'rerr: {abs(Edf-Emc)/Edf * 100} %')

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.2 s)
df: [1.74383742e-18]
mc: 1.74383742377e-18
rerr: [5.26145966e-11] %

Effective field#

[12]:

Hdf = 2 * A / (mm.consts.mu0 * Ms) * m.laplace
Hmc = mc.compute(system.energy.exchange.effective_field, system)
Hdf.allclose(Hmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.2 s)

[12]:

True

DMI (T)#

property

equation in continuous form

discretisedfield form

Energy density

\(w = D \mathbf{m} \cdot (\nabla \times \mathbf{m})\)

D * m @ m.curl

Energy

\(E = \int_{V} D \mathbf{m} \cdot (\nabla \times \mathbf{m}) dV\)

(D * m @ m.curl).volume_integral

Effective field

\(\mathbf{H}_\text{eff} = -\frac{2D}{\mu_{0}M_\text{s}} (\nabla \times \mathbf{m})\)

- 2 * D / (mu0 * Ms) * m.curl

Energy density#

[13]:

wdf = D * m.dot(m.curl)
wmc = mc.compute(system.energy.dmi.density, system)
wdf.allclose(wmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.2 s)

[13]:

True

Energy#

[14]:

Edf =(D * m.dot(m.curl)).integrate()
Emc = mc.compute(system.energy.dmi.energy, system)
print(f'df: {Edf}')
print(f'mc: {Emc}')
print(f'rerr: {abs(Edf-Emc)/Edf * 100} %')

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.2 s)
df: [-4.35058832e-18]
mc: -4.35058832385e-18
rerr: [-7.88329253e-11] %

Effective field#

[15]:

Hdf = - 2 * D / (mm.consts.mu0 * Ms) * m.curl
Hmc = mc.compute(system.energy.dmi.effective_field, system)
Hdf.allclose(Hmc)

Running OOMMF (ExeOOMMFRunner)[2023/10/23 16:08]... (0.3 s)

[15]:

True

(Oversimplified) micromagnetic calculator#

Here we try to implement an (oversimplified) micromagnetic calculator we had a look at in the first session:

a6a0939fb8794d7a83e85c8052b4116f

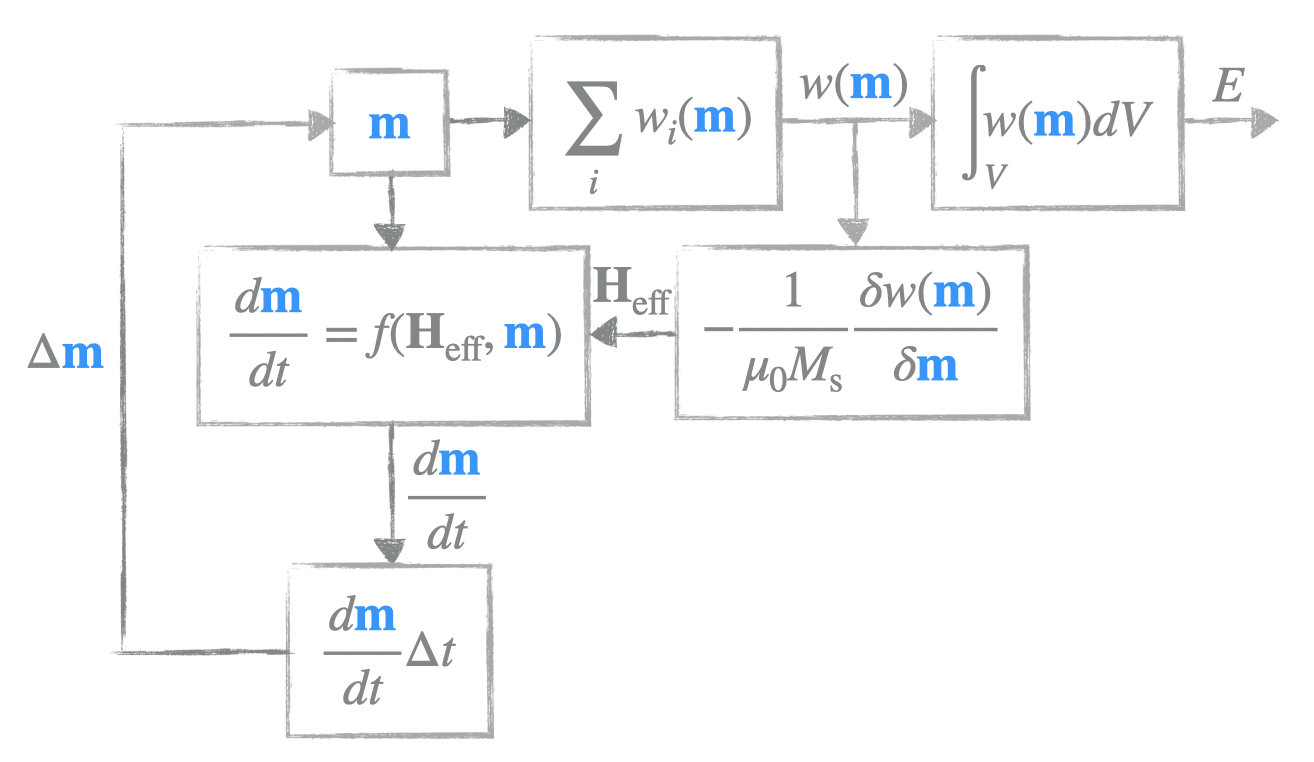
We start by defining some basic parameters:

[16]:

# Geometry
L = 100e-9
thickness = 5e-9
cell = (5e-9, 5e-9, 5e-9)
p1 = (-L/2, -L/2, 0)
p2 = (L/2, L/2, thickness)
region = df.Region(p1=p1, p2=p2)
mesh = df.Mesh(region=region, cell=cell, bc='xy')

# Material parameters
Ms = 3.84e5
A = 8.78e-12
D = 1.58e-3
K = 1e4
u = (0, 0, 1)
H = (0, 0, 1e5)
alpha = 1

def m_initial(point):
    x, y, z = point
    if x**2 + y**2 < (L/4)**2:
        return (0, 0, -1)
    else:
        return (0, 0, 1)

# Magnetisation field (M=Ms*m)
M = df.Field(mesh, nvdim=3, value=m_initial, norm=Ms)

M.sel('z').z.mpl()
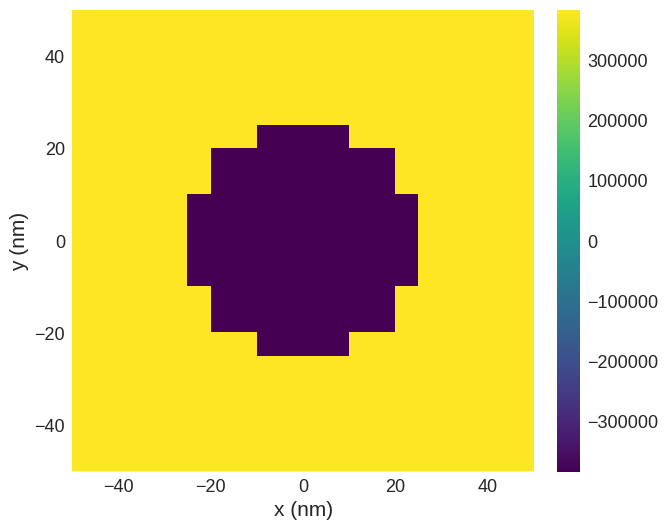
../../_images/examples_notebooks_field-operations2_31_0.png

Up to this point, everything should be exactly the same as we saw previously.

In the next step, we are going to implement functions which we are going to use to compute effective field and magnetisation time-derivative. The effective field we want is:

\[\mathbf{H}_\text{eff} = f(\mathbf{m}) = \frac{2A}{\mu_{0}M_\text{s}} \nabla^{2} \mathbf{m} - \frac{2D}{\mu_{0}M_\text{s}} (\nabla \times \mathbf{m}) + \frac{2K}{\mu_{0}M_\text{s}} (\mathbf{m} \cdot \mathbf{u})\mathbf{u} + \mathbf{H}\]

Dynamics equation we are going to use consists only of Damping term (in order to make simulations faster):

\[\frac{d\mathbf{m}}{dt} = f(\mathbf{m}, \mathbf{H}_\text{eff}) = -\frac{\gamma_{0}\alpha}{1+\alpha^{2}} \mathbf{m} \times (\mathbf{m} \times \mathbf{H}_\text{eff})\]
[17]:

def Heff_function(m):
    return (2 * A / (mm.consts.mu0 * Ms) * m.laplace -
            2 * D / (mm.consts.mu0 * Ms) * m.curl +
            2 * K / (mm.consts.mu0 * Ms) * (m.dot(u)) * u +
            df.Field(mesh, nvdim=3, value=H))

def dmdt_function(m, Heff):
    return -(mm.consts.gamma0*alpha)/(1+alpha**2) * m.cross(m.cross(Heff))

Now, we can try to perform the time integration, so that at each step we update our magnetisation:

\[\mathbf{m}_{i+1} = \mathbf{m}_{i} + \frac{d\mathbf{m}_{i}}{dt} \Delta t\]

So, our ubermag time driver would be:

[18]:

T = 0.1e-9  # simulation time (s)
n = 100  # number of steps
dt = T/n

for i in range(n):
    m = M.orientation
    m += dmdt_function(m, Heff_function(m)) * dt
    M = df.Field(mesh, nvdim=3, value=m, norm=Ms)

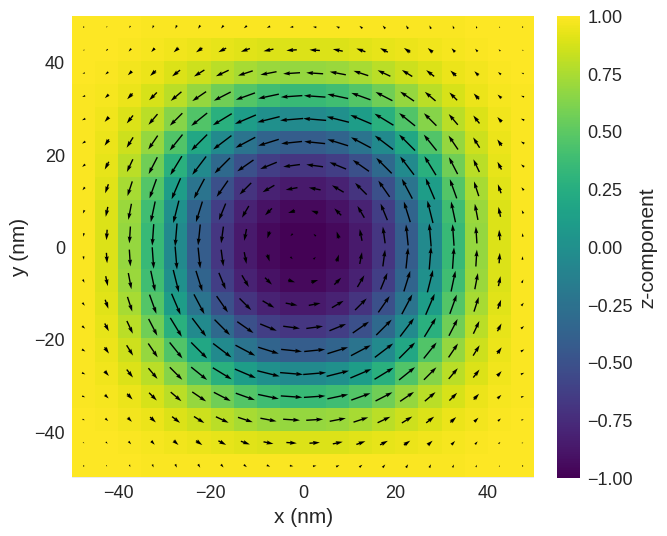
Finally, we can plot the magnetisation:

[19]:

M.sel('z').mpl()
../../_images/examples_notebooks_field-operations2_37_0.png