Simulation at finite temperature

Xf_ThermHeunEvolver

tutorial comming soon

Xf_ThermSpinXferEvolver

tutorial comming soon

UHH_ThetaEvolver

This tutorial demonstrates the use of the UHH_ThetaEvolver for simulations at finite temperature (based on the example mif file published as part of the relevant OOMMF extension).

import discretisedfield as df
import micromagneticmodel as mm
import oommfc as mc

We define the system object and specify the temperature 60K.

system = mm.System(name="thetaevolve", T=60)

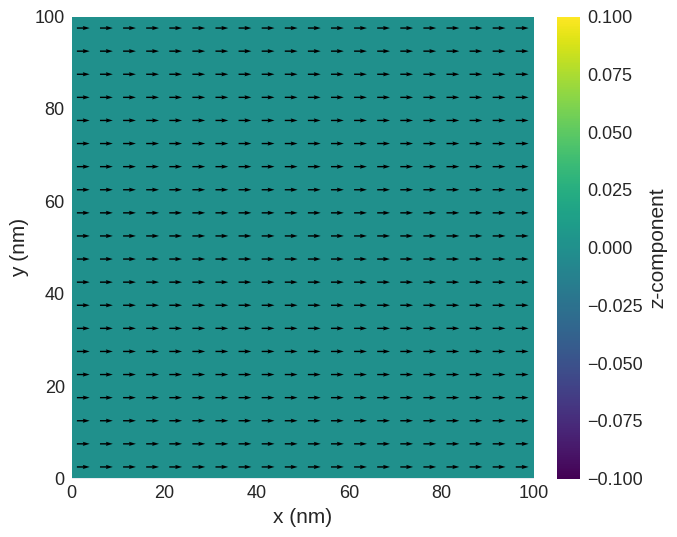
The simulation is done on a square geometry. The magnetisation is initialised uniformly pointing in x direction.

mesh = df.Mesh(p1=(0, 0, 0), p2=(1e-7, 1e-7, 1e-9), cell=(1e-9, 1e-9, 1e-9))
system.m = df.Field(mesh, nvdim=3, value=(1, 0, 0), norm=1700e3)

system.m.sel("z").resample(n=(20, 20)).mpl()

system.dynamics = mm.Damping(alpha=0.1) + mm.Precession(gamma0=mm.consts.gamma0)
system.dynamics

$-\frac{\gamma_{0} \alpha}{1 + \alpha^{2}} \mathbf{m} \times (\mathbf{m} \times \mathbf{H}_\text{eff})-\frac{\gamma_{0}}{1 + \alpha^{2}} \mathbf{m} \times \mathbf{H}_\text{eff}$

system.energy = mm.Exchange(A=1e-12)

We must explicitely specify the correct evolver and specify the timestep. For more details on how to specify this timestep as well as other available options please refer to the official documentation of the OOMMF extension available at http://www.nanoscience.de/group_r/stm-spstm/projects/temperature/download.shtml.

evolver = mc.UHH_ThetaEvolver(fixed_timestep=2e-13)

We can now use the previously defined evolver as input for the time driver.

td = mc.TimeDriver(evolver=evolver)

We drive the system for 0.5 ns and store the output in 50 steps.

td.drive(system, t=5e-10, n=50)

Running OOMMF (ExeOOMMFRunner)[2024/08/09 17:20]... (3.6 s)

We can now plot the magnetisation after time driving.

system.m.sel("z").resample(n=(20, 20)).mpl()

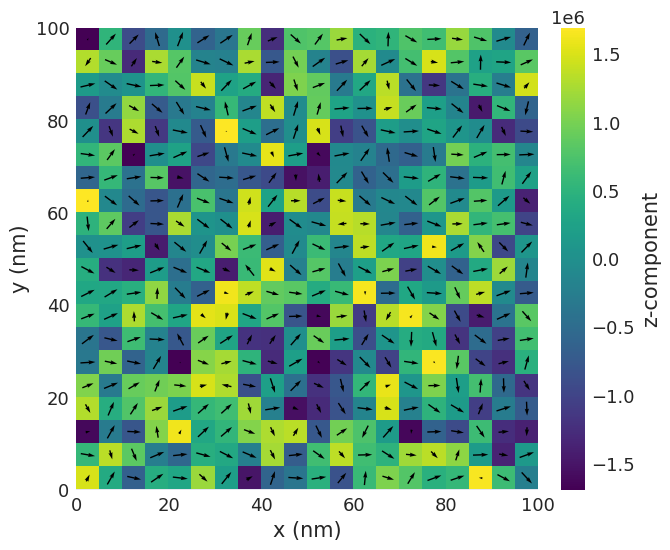
Information about the individual steps is available from the table object.

system.table.data.head()

	E	E_calc_count	max_dmdt	dE/dt	delta_E	T	E_exchange	max_spin_ang_exchange	stage_max_spin_ang_exchange	run_max_spin_ang_exchange	iteration	stage_iteration	stage	mx	my	mz	last_time_step	t
0	1.120473e-17	51.0	94556.924744	-0.000002	1.424474e-19	60.0	1.120473e-17	139.657090	139.657090	139.657090	50.0	50.0	0.0	0.858284	-0.000984	0.004200	2.000000e-13	1.000000e-11
1	1.659172e-17	102.0	111424.756023	-0.000002	7.302315e-20	60.0	1.659172e-17	165.993223	177.321519	177.321519	101.0	50.0	1.0	0.779396	-0.000714	0.008684	2.000000e-13	2.000000e-11
2	1.886557e-17	153.0	97915.624174	-0.000002	3.477843e-20	60.0	1.886557e-17	170.565176	177.967891	177.967891	152.0	50.0	2.0	0.738897	0.000991	0.004611	2.000000e-13	3.000000e-11
3	2.001070e-17	204.0	97996.465424	-0.000002	3.091047e-20	60.0	2.001070e-17	176.614042	179.480712	179.480712	203.0	50.0	3.0	0.714047	-0.002506	0.006134	2.000000e-13	4.000000e-11
4	2.038523e-17	255.0	97941.958430	-0.000002	3.478005e-20	60.0	2.038523e-17	175.466903	179.097395	179.480712	254.0	50.0	4.0	0.700108	-0.004356	0.002749	2.000000e-13	5.000000e-11

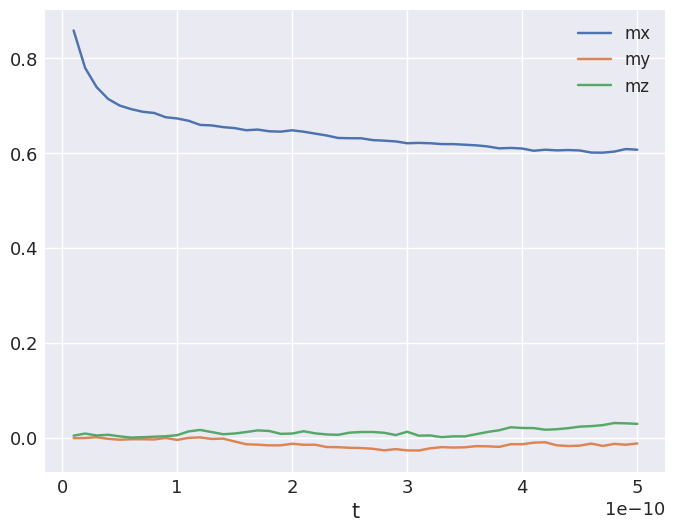
We can plot the average magnetisation as a function of time.

system.table.data.plot(x="t", y=["mx", "my", "mz"], grid=True);